14. 3 载流量计算
D. H. Simmons 博士在 1925 年发表了一系列论文 “ Calculation of the Electrical Problems in Underground Cables ( 地下电缆的电气参数的计算)”[9] , 1932 年又进行了修改。 美国国家电气照明协会 ( NELA) 1931 年首次出版了 PILC 电缆在沟槽或空气中敷设情况下载流量表格。 1933 年, 爱迪生电气学会 ( EEI) 把 NELA 的表格扩展到包括其他负载因数的情况。
1957 年 6 月, Jack Neher 和 Martin McGrath 发表的经典论文为载流量计算作出了突出的贡献[10] 。 AIEE- IPCEA 的黑皮书[1] 中的载流量表格就是采用上述论文中的方法计算的。 后来, 在 1995 年, IEEE 又修订和再版了上述书籍[11] 。 IEEE 还用电子版的形式出售相应的计算表格[12] 。
在稳态情况下, 热传播的基础理论与欧姆定律相同, 热流与温度成正比, 与热阻成反比, 见下式。
![]()
el
th
I = TC R- T×A -R ΔTd × 10 - 3 (14- 1)
式中, I 为要计算的电流值 ( A); TC 为最高允许导体温度 ( ℃ ); TA 为周围环境温度 ( ℃ ); ΔTd 为介质损耗产生的温升 ( ℃ ); Rel为温度 TC 时导体电阻 ( Ω / ft);
Rth 为从导体到环境的热阻 ( 热欧姆 英尺)。
14. 3. 1 热路模型
电缆材料既存储热也传导热。 运行时, 产生了热流。 热既存储在电缆的各个组成部分, 同时又从高温区向低温区传导。 上述情况的简单热路等同于 R- C 电路,如图 14- 1 所示。
时刻 t = 0, 开关合上, 最初所有的热都由电容吸收。 根据 R 和 C 的数值, 随
着时间的流逝, 电容充满后, 所有的电流都流过电阻。 因此, 对时间常数大的电缆, 短时负载时热容必须要考虑 ( 见本章 14. 4 节)。
14. 3. 2 负载因数
平均负载与峰值负载的比率称为负载因数。 这是一个很重要的参数。
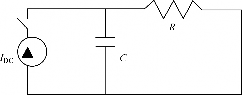
图 14- 1 简单热路
在公共电网中, 一天之内负载变化很大。 周期性负载对载流量计算的影响取决于环境的热容参数。
沟道中或直埋地敷设的电缆周围存在巨大的热容。 沟道、 混凝土和埋地的电缆都需要时间热起来 ( 以及冷却下来) 。 因此, 负载升高时环境会吸收热量, 载流量比持续负载要高。 同样, 在周期性负载的负载下降时, 冷却过程时环境也会放热。
对于小规格电缆在空气中或者空气中管道敷设的状况, 热的滞后效应很小。 电缆很快在 1 小时或 2 小时会热起来。 对于通常峰值负载持续超过 2 小时的周期性负载, 在载流量计算时不用考虑负载因数。
14. 3. 3 损耗因数
已知日负载因数时, 可以利用下式计算损耗因数:
LF = 0. 3( lf) + 0. 7( lf) 2 (14- 2)
式中, LF 是损耗因数; lf 是日负载因数。
在离电缆中心一定距离时, 损耗因数成为重要参数。 Neher 和 McGrath 推导的这个假想距离 Dx 为 8. 3in (211mm)。 超过这个距离后, 热效应减弱, 损耗因数开始起作用。
14. 3. 4 导体损耗
电流流过材料时, 就会产生电阻。 这是每种材料的固有特性, 可以用电阻率表示。 电阻率的倒数是电导率。 选择导体材料时, 希望采用电阻率低的材料, 同时这种材料不太贵又容易加工。
铜和铝是电力电缆应用的两种理想材料, 在世界上已经广泛使用。
除了要选择电缆的金属材质, 还要面对电阻的计算。 为了计算电缆载流量, 需要确定导体电阻。 导体损耗的计算具体请看第 3 章。
14. 3. 4. 1 导体直流电阻
本节内容在第 3 章已经涉及。 这里主要增加载流量计算需要的内容。 20℃ 时退火铜的体积电阻率如下 ( 见表 14- 1):
ρ20 = 0. 017241 Ω mm2 / m (14- 3)
另一种单位表示如下:
ρ20 = 10. 371 Ω cmil / ft (14- 4)
导体的电导率表示为与一个标准值相比的百分相对值。 国际电工委员会
( IEC) 在 1913 年确立了国际退火铜标准 ( IACS)。 退火铜的电导率确定为 100% 。
表 14- 1 20℃时直流电阻率
金 属 | 电 导 率 | 电 | 阻 | 率 | 重量电阻率 |
百分比 IACS | Ω cmil / ft | Ω mm2 / m | Ω lb / mile2 | ||
软铜 | 100. 00 96. 16 39. 21 61. 2 53. 5 52. 5 20. 33 5 | 10. 371 10. 785 26. 45 16. 946 19. 385 19. 755 51. 01 129. 64 | 0. 017241 0. 01793 0. 043971 0. 02817 0. 03223 0. 03284 0. 08401 0. 21551 | 875. 2 910. 15 2046. 3 434. 81 497. 36 506. 85 3191. 0 9574. 0 | |
硬铜 | |||||
铜包钢 | |||||
1350- H19 铝 | |||||
5005- H19 铝 | |||||
6201 T81 铝 | |||||
铝包钢 | |||||
钢 | |||||
(53. ,
与退火铜导体比较, 铝导体的典型电导率是 61. 2% 。 因此, # 1 / 0 AWG 5mm2 ) 实心 61. 2% 铝导体的体积电阻率是 16. 946Ω cmil / ft 截面积是
105600cmil。 在 20℃ 时 1000ft 的直流电阻 ( DC) 计算如下:
RDC (20) = 16. 946 × 1000 / 105600 = 0. 1605Ω
换算到其他常用温度采用下列公式:
RT2 = RT1 [1 + α( T2 - T1 )] (14- 5)
式中, RT2 为计算温度下导体直流电阻; RT1 为基准温度下导体直流电阻; α 为电阻温度系数。
不同铜铝导体在各个基准温度下的温度系数见表 14- 2。
14. 3. 4. 2 导体交流电阻
导体交流 ( AC) 电阻就是直流电阻加上电流密度不均匀导致的集肤效应产生的电阻增量。 集肤效应使在导体内部的电流密度减少。 导体中心的纵向磁力线比边缘部位的大大增加。 逆电动势在中心区域更大。 由于电流密度的减少, 中心区域的净电动势也减少了。
有许多论文和报告提出了计算交流电阻增量的方法, 参考文献 [10] 是一个例子。
表 14- 2 导体金属的电阻温度系数
金 | 属 | 0℃ | 20℃ | 25℃ | 30℃ |
61. 2% 铝 | 0. 00440 | 0. 00404 | 0. 00396 | 0. 00389 | |
100. 0% 铜 | 0. 00427 | 0. 00393 | 0. 00385 | 0. 00378 | |
98. 0% 铜 | 0. 00417 | 0. 00385 | 0. 00378 | 0. 00371 | |
96. 0% 铜 | 0. 00408 | 0. 00377 | 0. 00370 | 0. 00364 | |
导体的电力线会受到附近电流的影响, 在横截面上产生电流分布不均匀, 就像导体本身产生的那样。 这种情况叫做邻近效应。 集肤效应和邻近效应不能分开, 之间也不是直接叠加的关系。 如果导体间距超过导体外径的 10 倍以上, 就可以忽略邻近效应。
14. 3. 4. 4 磁滞和涡流效应
导体和邻近的金属部件的磁滞和涡流损耗能增加交流电阻。 为了满足这些损耗, 电缆需要消耗更多的功率。 当导体载流量很大, 并且磁性金属层又紧挨着导体时, 磁滞和涡流损耗会变得非常大。 导体电流超过 200A 时, 要多考虑磁滞和涡流损耗。
14. 3. 5 介质损耗的计算
如第 4 章所示, 介质损耗对载流量影响很大。 对有屏蔽单芯导体或者分相屏蔽多芯导体的电缆, 介质损耗计算见下式:
Wd = 2πfCnE2 Fp × 10 - 6 (14- 6)
以及
C = 7. 354ε/ log10 ( DO / DI) (14- 7)
式中, f 为运行频率 ( Hz); n 为电缆中屏蔽导体根数; C 为单芯屏蔽导体的电容
( pF / ft); E 为对地电压 ( kV); Fp 为绝缘功率因数; ε 为绝缘介电常数; DO 为绝缘外径; DI 为绝缘内径。
14. 3. 6 金属屏蔽损耗
导体中有电流流过时, 就会产生相应的磁场。 如果电流的幅值随时间变化, 比如 60 Hz 交流电, 磁场强度就随着电流幅值变化。 此时, 如果有第二个导体位于导体电流产生的交变磁场中, 在第二个导体上就会产生随磁场变化的电压。
如果第二个导体在一个回路中, 感应电压就会产生电流。 在有金属屏蔽的导体通电运行时就会产生上述情况。 每相导体的电流会在所有处于磁场中电缆的金属屏蔽中感应电压。 如果这些屏蔽有 2 个以及更多点接地或者构成回路, 在金属屏蔽中就会产生电流。
金属屏蔽中的这些电流会产生损耗。 损耗的大小取决于屏蔽电阻和电流幅值。 这些损耗表现为热损耗。 这些损耗不仅费电, 而且对载流量和电压降都会产生不利影响。 与导体损耗和介质损耗一样, 屏蔽产生的热损耗也要散出去。 由于特定环境的散热能力是固定的, 屏蔽产生的热损耗就会降低导体热损耗的散失, 从而会减少导体的载流能力。 换句话说, 屏蔽损耗减少了载流量。
多芯回路时, 任一屏蔽中的感应电压与所有连接屏蔽的磁力线总和有关。 由于在一个平衡的多回路系统中, 总电流等于零, 当三相的屏蔽线等距对, 一个平衡的多回路系统中, 总电流也等于零。 通常, 回路是不平衡的, 实际上会有一些磁通在屏蔽中产生感应电压/ 电流。 在单芯有屏蔽导体的电缆安装时, 随着导体间距的增加, 其他导体产生的磁通随之减少。 电缆每相屏蔽上总的磁通相当于该相导体的磁通 ( 见图 14- 2)。
随着间距 S 的增大, B 相和 C 相的影响在减小, A 相导体的金属屏蔽损耗几乎完全来自 A 相电流的磁通。
有 2 个方法可最大限度减少屏蔽损耗的数值:
● 单点接地 ( 屏蔽开路)。
● 减少屏蔽中使用金属的量。
屏蔽开路会有其他的麻烦。 感应电压从接地点开始逐渐增大, 在远离接地点的最远端达到最大值。 感应电压的幅值基本上取决于导体电流。 有两个电流数值是必须考虑的: 系统设计的最大运行电流和最大故障电流。 感应电压的数值取决于安全要求以及护套设计。
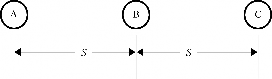
图 14- 2 临近效应
另一个途径是减少屏蔽中的金属物。 由于回路是 1∶ 1 的变压器, 屏蔽电阻的增加会减少屏蔽感应电流的幅值。 例如, 铝导体, 截面积 507mm2 , 三相, 15kV, 分相中性线水平间距 190. 5mm 敷设。 中性线电导率为导体 1 / 3 的电缆感应电流是中性线电导率为导体 1 / 12 的电缆的 4 倍。 假设平衡的各相电流为 600A, 屏蔽中电流会达到 400A。 中性线电导率为 1 / 12 的相同电缆的感应电流只有 100A。 总电流从
1000A 下降到 700A。 对减少屏蔽金属量的电缆, 载流量能够增加 25% 左右。
为了在计算载流量时考虑屏蔽损耗, 需要用 1 加上屏蔽损耗与导体损耗的比值后再乘以热路中屏蔽以外的所有热阻。 这个热阻增量就反映了屏蔽损耗的影响。
其他结构电缆的屏蔽损耗的计算很复杂, 但是也很重要。 对单芯电缆的一些结构, Halperin 和 Miller 研究了一个非常近似的方法计算屏蔽损耗和感应电压。